贪心算法1
17 Jun 2013 by LelouchHe
本系列起源
正如上一篇博文所说的,试图利用空闲时间看完算法之美有些不太现实,所以我做了决定,只看中文书和kindle这种可以随时随地可读的东东.
这一个系列的文章应该原自Algorithms Design,是从kindle上读的,有一段时间了,所以觉得应该写些东西来巩固下.
你可以把这系列东西看作是书的中文简写,当然,里面还有杂七杂八的一对个人想法
简单Interval Scheduling问题
问题很简单,有若干任务,每个任务包含其起止时间(s_i和f_i),我们有一段从s到f的时间可以拿来处理这些任务,这些任务不能重叠处理,即各自的处理时间不能有重叠(同一时间只能处理一个任务).目标是如何安排这些任务的处理顺序,使得这段时间内可以处理的任务最多
第一眼的想法
最最naive的想法是,恩,我先把s_i < s和f_i > f的任务从总任务中剔除.这个应该是最直观的想法了.我们假设剩下n个任务,他们的起止时间都在指定的范围之内,也就是理论上可以完成的任务.
问题的难点就是如何从这n个任务挑选出最多的任务.
怎么贪心
在贪心系列里讲问题,肯定是用贪心算法来解(不过不要想当然,我会是不是腹黑一下的..).目前问题的症结在于,即使确定了使用贪心,仍然有很多贪心的方向和角度待选.
正如书中所言,我们可能会有以下几个很自然的方向:
- s_i: 即每个任务的开始时间,自然,我们每次选择当前剩余任务集合中最早的任务i,然后把矛盾(时间上有重叠)的剔除,在剩下的集合中重复此操作,直到集合为空
- f_i: 即每个任务的结束时间,过程同上
- f_i - s_i: 即每个任务的持续时间,过程同上
- 与其他任务重叠最少的任务i: 每个任务都有和其他任务的重叠数(不重叠就是0),我们每次都挑选与其他任务重叠最少的任务,然后过程同上
可以看到,这些方向的一个特点是都有最,而且都选最.这其实是贪心,我们每次的选择都是在某个方向上的一个极点,然后不停的选择这个极点,然后期望得到一个全局的最优.
这个很类似机器学习中的梯度下降(Gradient Descent),当然,面临的问题也是一致的:怎么能保证一个局部的最优可以带来全局的最优?
具体来说,分解为两个问题:
- 局部/全局并不是在一个方向上的最优,就好像上面的4个方向,局部最优都是最早/最晚/最短/最少,但寻找的全局最优却是最多.其实这之中有一个转换的过程,我们希望挑选每个最早的任务,让剩下的时间多些,然后就可以处理更多的任务.看到没,这是一个转换.处理问题时,时刻牢记一点,我们寻找的是全局,而非局部,不要车现在局部而忽略了真正的目标
- 局部产生全局的过程:我们如何保证每次挑选的局部最优能在最后产生一个全局最优.试想一个最naive的情况,我们试图找到一系列整数的最大和,我们每次挑选一个最大值,这样的结果必然会给我们一个全局的最大值(好吧,这个太简单了).但也有局部产生不了全局的例子,比如上面那个问题中的方向1,很有可能的情况时,最早开始的任务非常长,结果整个时间短只能处理这一个任务了,那么这肯定不是全局下最多的任务数
探索问题
上面的两个问题,指引了两个角度,或者步骤:
- 局部贪心同”全局最优“的递推(有的时候局部的方向是错的,得不到全局,所以我加了引号).我们要给出合适的局部贪心,这样的贪心至少在方向上可能产生全局的最优结果.比如如果我们找了一个方向是持续时间最接近质数的任务,当然,这个也可算是贪心(虽然比较奇怪),但这样的贪心无法合理的带来全局的最多(质数和最多任务有毛线关系啊摔)
- 局部贪心可以推导出全局最优.这个看起来很像第一个,但是有些许区别.第一个角度主要提示我们思考的方向,第二个角度则是要我们给出对应的证明,来证明此贪心方向可行(it works)或不可行(it sucks)
这两个步骤哪个更难呢?
其实都难.
对于第一个步骤,我们可能会有很多自然的贪心方向,但不一定每个都是可能的方向(甚至可能没有一个方向是正确的,如果我们很搓的话)
对于第二个步骤,我们则要努力的进行证明,递推也好,反证也好,总之要搞出来.
不过可能更难的一个步骤我没有提到,就是什么问题才能用贪心求解,很有可能我们试图贪心了很久,结果发现这个问题是无法贪心的,那就悲剧了.(这个问题等我们综合了很多算法的问题和经验后可能才有答案,等等吧)
关于本问题
那么本问题的至少四个可能的方向中,哪个才是我们真正可以利用的呢?
其实,除去2(即f_i)的方向,其他方向我们都是很容易找到反例的,与其证明一个方法可行,不如证明一个方法是错误的简单.这也是在贪心和其他算法设计中经常用到的反证法,不过这个方法只有在试图证明错误,或者已经找到正确解的前提下才能使用,真是非常遗憾.
至于方向2,选取最早结束的任务(按照f_i贪心),如何证明它可以带来全局最优解呢?这里可以使用的一个常用的论证方法是”stay ahead”.顾名思义,就是需要证明贪心的每一步,都比可能的最优的结果要优,一直”stay ahead”,所以最后的结果也是全局最优.
这么说可能有些抽象,我们来看图解释.假设G(Greedy)是我们通过贪心的得到的解G_i是其中第i个任务,B(Best)是一个我们不知道的真正的全局解,B_i是其中第i个任务.我们通过以下归纳方法证明:
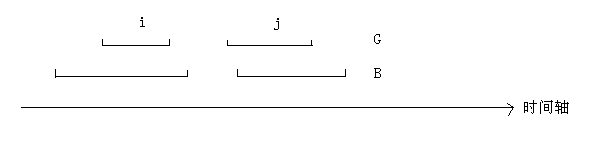
- f(G_0) <= f(B_0),这个是显而易见的,因为G本来最先挑选的就是最早结束的任务,所以G_0肯定比B_0结束的早
- 假设这种关系在第i个任务时也成立,即f(G_i) <= f(B_i),我们需要证明f(G_j) <= f(B_j),其中j = i + 1.由于f(G_i) <= f(B_i),可得f(G_i) <= f(B_i) <= S(B_j),所以G_i和B_j是不重叠的,这样,我们假设f(G_j) > f(B_j),那么目前的贪心算法肯定会选择B_j,而不是G_j的(因为我们选择的是不重叠的最早结束的任务),矛盾,所以得证
- 所以,可以看到,G和B可以一一对应起来,而且一直f(G_i) <= f(B_i),这样,G的最后一个任务一直比B早,这样可以保证G的数量至少同B一样多(如果G结束之后还有空余,则G的数量比B多)
stay ahead
stay ahead的基本操作就是这样的,起始于一个合理的初始情况(i = 0),然后证明在其他情况下,贪心的当前结果不比一个最优结果(这个是假设的未知,仅用于证明)的当前结果差,然后最容易忽略的一步,就是证明,这样的”stay ahead”可以带来全局的最优,即把每次的”stay ahead”可以得到全局的最优结果.
正如上面第3步那样,我们每步证明的G比B早结束,但是早结束并不代表总的任务数多,所以我们还是必须加以证明,才能完善我们的论证,这三步一个都不能少.
代码
struct task_t
{
int s;
int f;
};
int task_cmp(const void *a, const void *b)
{
const struct task_t *t_a = (const struct task_t *)a;
const struct task_t *t_b = (const struct task_t *)b;
return t_a->f < t_b->f;
}
int interval_scheduling(struct task_t tasks[], int task_num)
{
qsort(tasks, task_num, sizeof (struct task_t), task_cmp);
int num = 0;
int i = 0;
while (i < task_num)
{
num++;
j = i + 1;
while (j < task_num)
{
if (tasks[i].f <= tasks[j].s)
{
break;
}
j++;
}
i = j;
}
return num;
}
总结
其实所有的贪心问题,都应该有一个底层的理论相通处,比如虽然我们可以使用”stay ahead”和反证法来证明贪心的正确性,但是这并没有告诉我们为什么.证明是事后诸葛亮,但并不能告诉我们事前是什么样子的.
不过可惜的是,目前我还没有找到贪心问题的底层结构,算法导论上好像有类似的阐述,我还没有看明白,希望在贪心的最后一个系列可以完成这样的解释